索引
1. 基本概念
索引(index):是一种数据结构,通过记录搜索码和维护一个指向表中数据的指针或引用,使得查询操作可以跳过全表扫描,直接定位到目标数据,用于快速查找数据库表中的特定记录
| 类型 | 顺序索引(Orderd) | 散列索引(Hash) |
|---|---|---|
| 操作 | 按照搜索码的值进行排序 | 按照搜索码的散列函数值将数据分布到多个桶中 |
| 适用 | ORDERD BY和BETWEEN | =和IN |
| 优势 | 适合范围查询,时间复杂度高 | 适合精准查询,时间复杂度低 |
| 劣势 | 插入和删除操作的成本高 | 破坏了顺序信息 |
2. 顺序索引
2.1 聚集和辅助
| 类型 | 聚集索引(Clustered ) | 辅助索引(Secondary) |
|---|---|---|
| 定义 | 数据顺序与索引顺序一致 | 数据存储顺序与索引顺序无关 |
| 特性 | 一个表只能有一个聚集索引 | 一个表可以有多个辅助索引 |
| 适用 | 范围查询 | 多条件查询 |
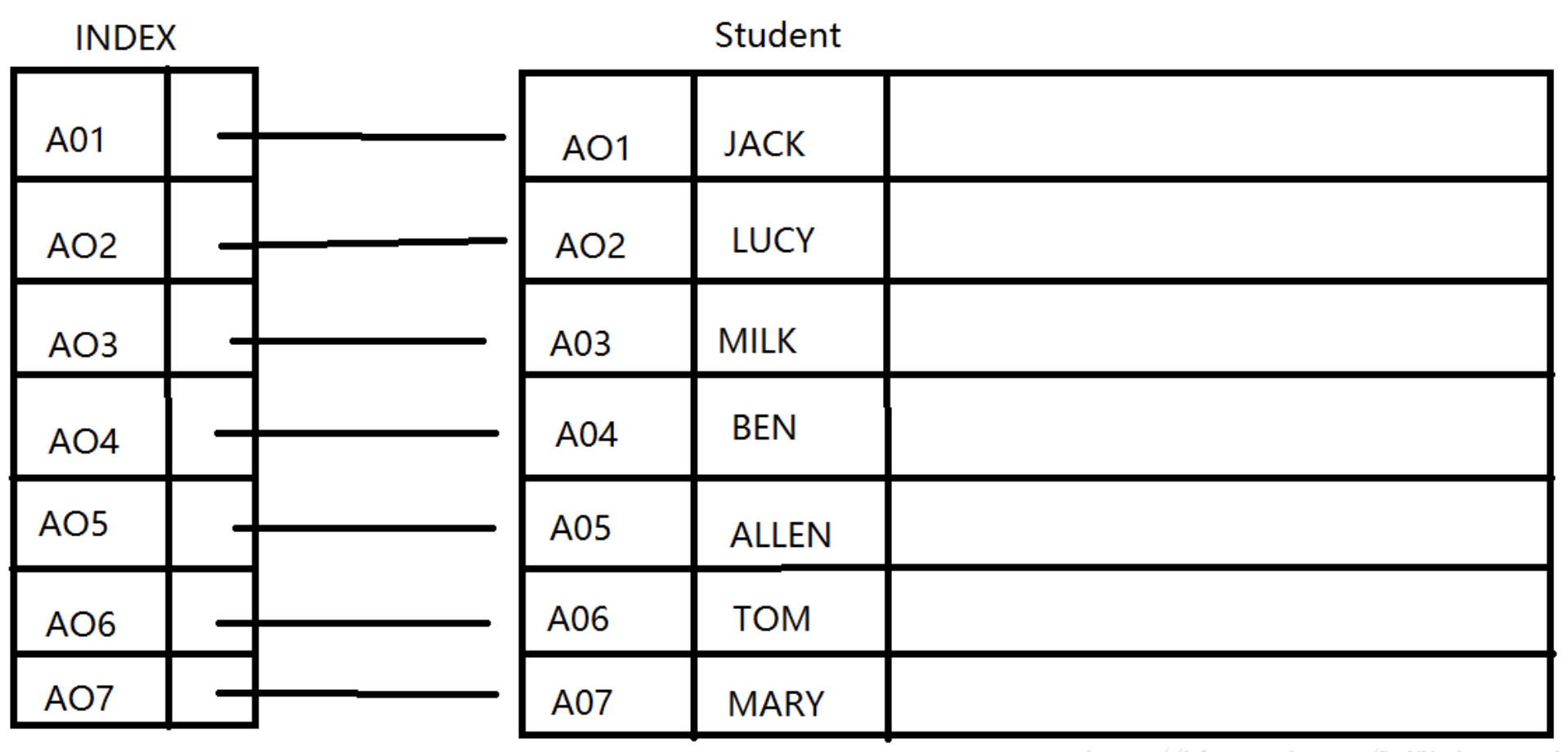
聚集索引
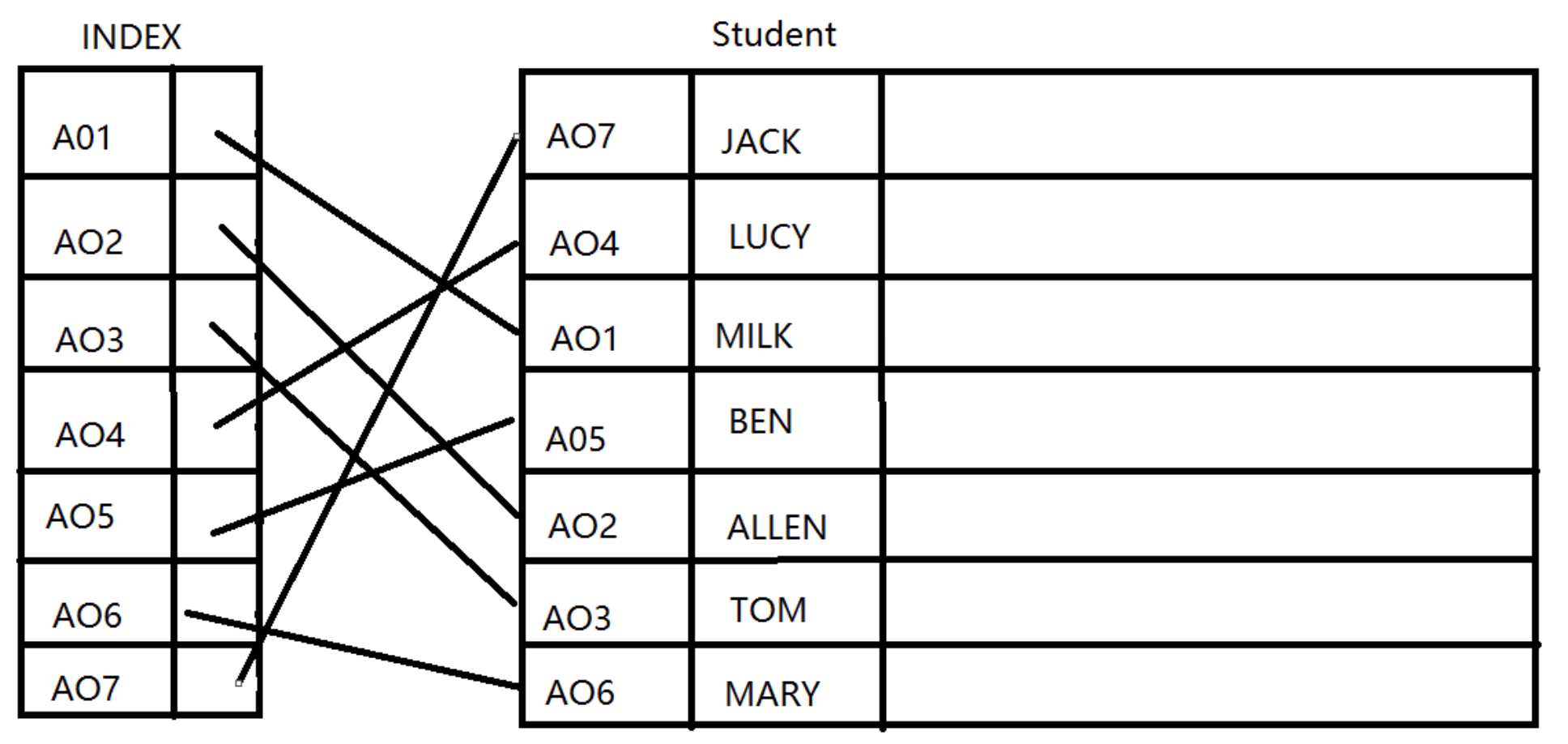
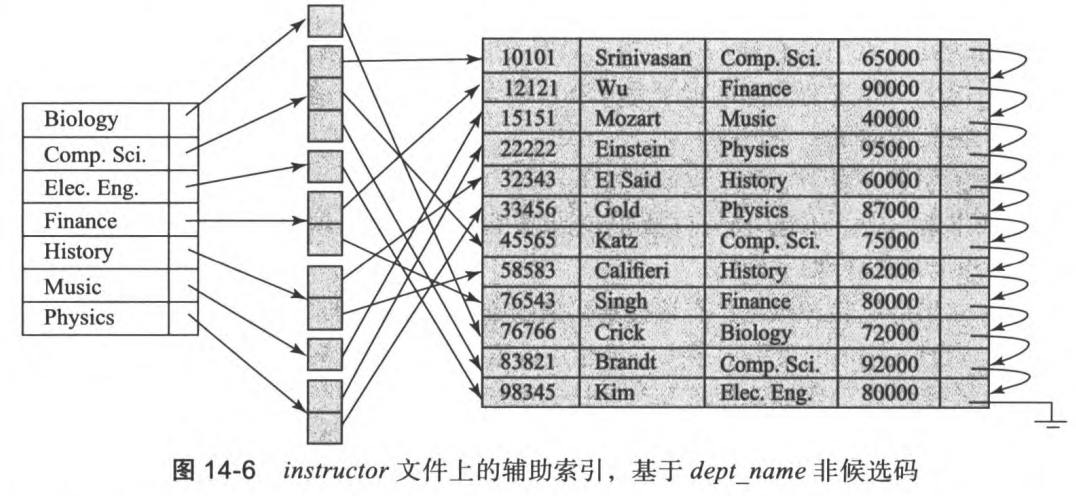
辅助索引
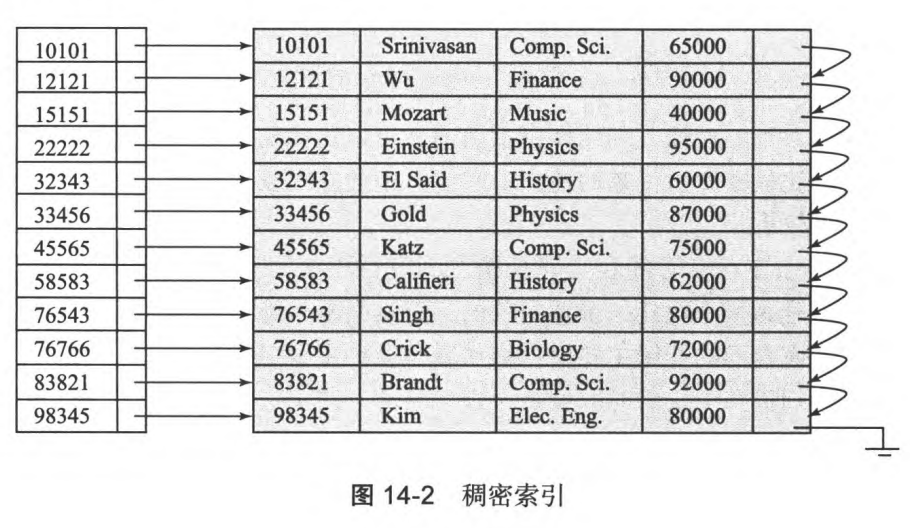
2.2 稠密和稀疏
| 类型 | 稠密索引(dense) | 稀疏索引(sparse) |
|---|---|---|
| 定义 | 每条数据都有索引 | 只有部分数据有索引 |
| 特性 | 辅助索引是稠密的 | 稀疏索引是聚集的 |
| 适用 | 等值查询 | 范围查询 |
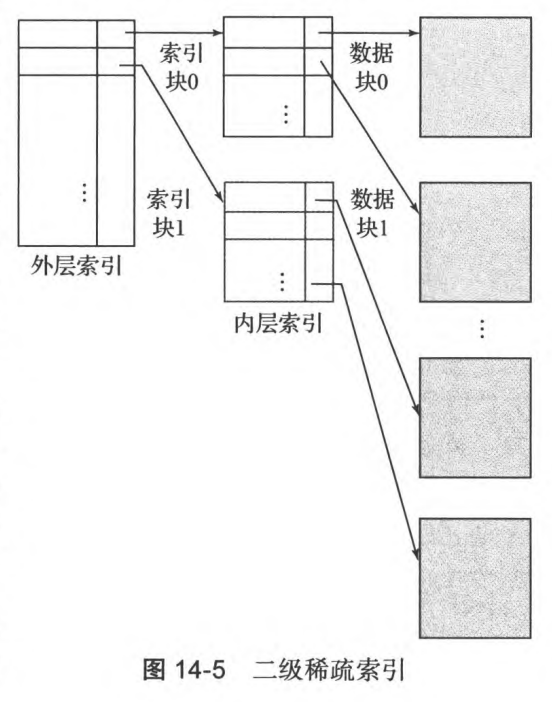
2.3 多级索引
多级索引:将索引结构分为多个层级,每一层索引都是对下一层数据的索引
2.4 桶索引
用于处理非唯一搜索码,索引包含指向桶的指针,每个桶包含指向记录的指针
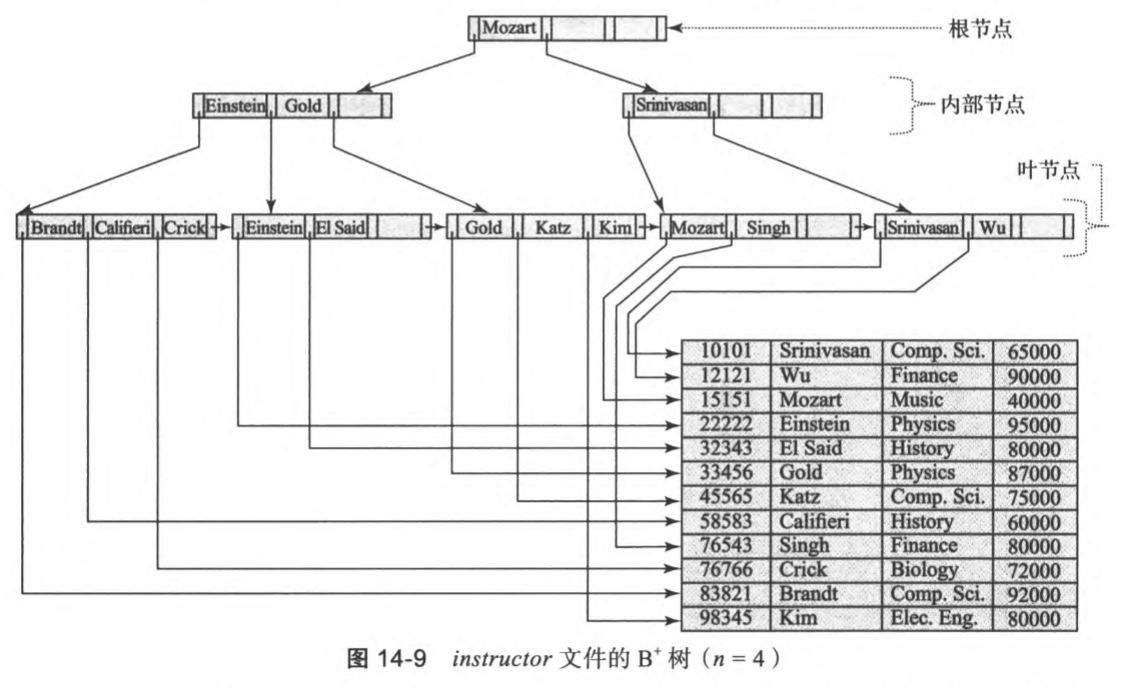
3. B+树索引
3.1 树结构
- 平衡性:所有叶子节点位于同一层
- 有序性:所有叶子节点按顺序从左到右连接,形成一个有序链表
- 内部节点/索引节点:存储指向索引的指针,用于引导搜索过程
- 叶子节点/数据节点:存储指向数据的指针
- 阶:节点最多可以拥有的孩子个数
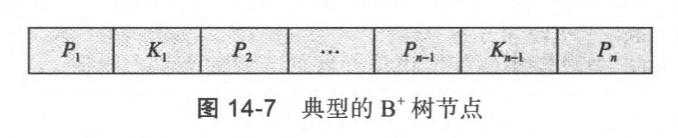
3.2 节点结构
若阶为n,则有:
- 非根非叶节点至少有个关键字
- 叶节点至少有个关键字
- 每个节点的指针数量总是比关键字数量多1
- 每个节点的关键字数量最多有n-1个
- 每个节点的指针数量最多有n个
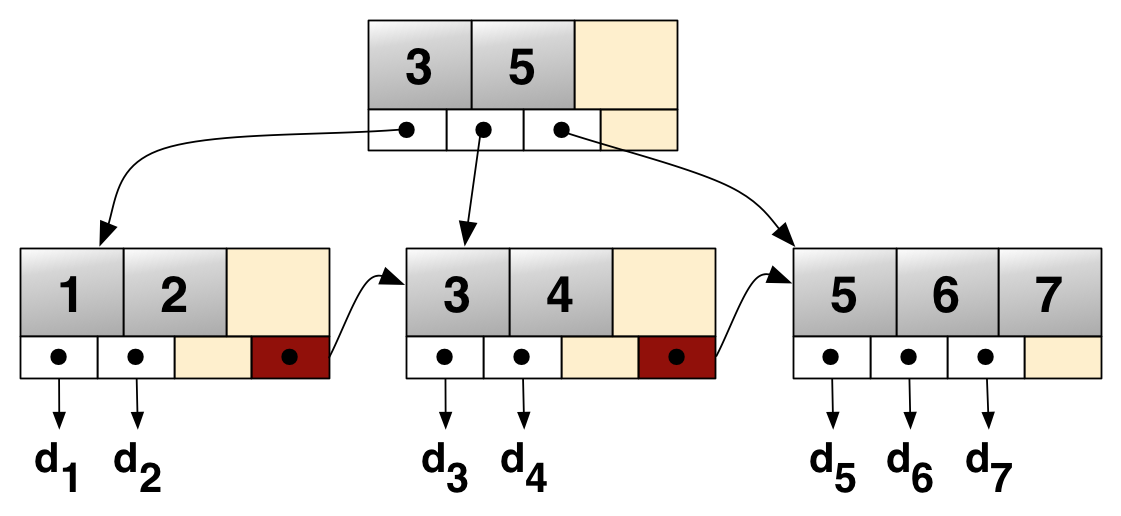
叶子节点:代表着稠密索引
- 指针指向具有关键字的一条文件记录
- 最后一个指针指向下一个叶子节点
内部节点:代表着多级稀疏索引
- 指针指向搜索码值小于的子树
- 指针指向搜索码值小于的子树
- 指针指向 搜索码值的子树
3.3 查找操作
假设每个节点的搜索码列表用key表示,指针列表用point数组表示,搜索码是value
- 从根节点开始
node = root - 在当前节点中找到满足
value <= node.key[i]的最小 i- 如果 i 不存在,则
node = node.point[-1] - 如果
value = node.key[i],则node = node.point[i+1] - 如果
value < node.key[i],则node = node.point[i]
- 如果 i 不存在,则
- 重复第2步直到叶子结点,找到满足
key[i] = value的 i,返回node.point[i]
实际上,B+树也可以在所有叶子节点组成的链表上遍历搜索,一种是随机查找,一种是顺序查找,前者适合单值查询,后者适合范围查询
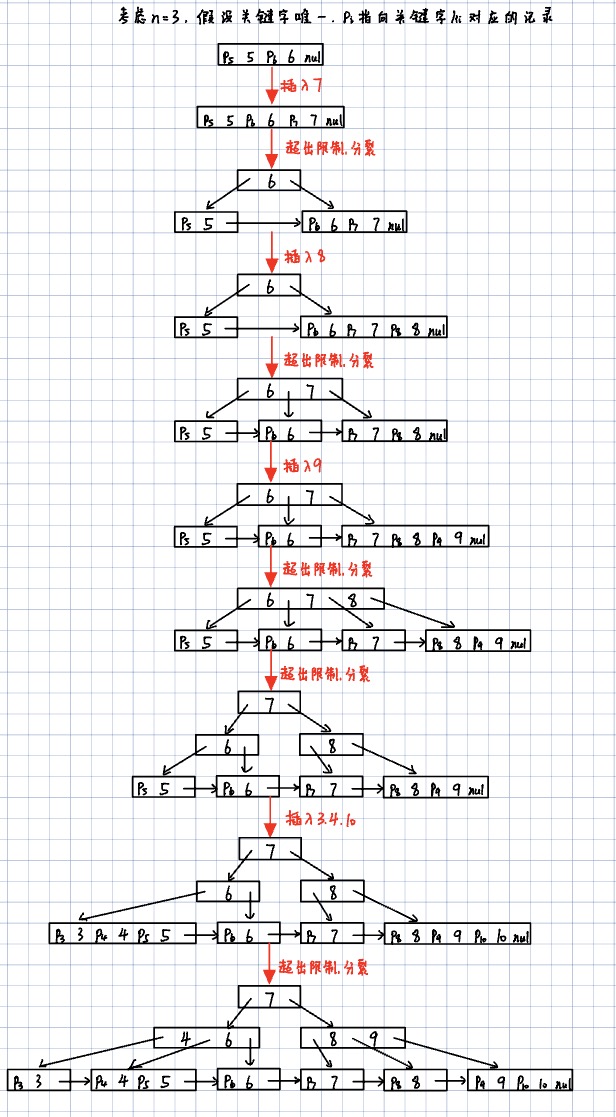
3.4 插入操作
- 寻找插入位置:根据关键字的顺序,从根节点出发,递归地查找合适的叶子节点,在该节点中插入新关键字
- 叶子节点插入:如果目标叶子节点此时关键字个数小于,则结束,否则进入第3步
- 叶子节点分裂:将这个叶子节点分裂成左和右两个叶子节点
- 左叶子节点包含前个关键字,右叶子节点包含剩下的关键字
- 将第个关键字插入到父节点中,其中该关键字的左边指针指向左叶子结点,右边指针指向右叶子节点
- 若当前父节点的关键字的个数小于n,则结束,否则进入第4步
- 内部节点分裂:将这个内部节点分裂成左和右两个内部节点
- 左内部节点包含前个关键字,右内部节点包含剩下的关键字
- 将第个关键字插入到父节点中,其中该关键字的左边指针指向左叶子结点,右边指针指向右叶子节点
- 递归执行上述过程直到结束或者父节点是根节点,进入第5步
- 创建新根节点:将原根节点的第个关键字提升到新根节点,令新根节点的左指针指向分裂后的左子节点,右指针指向分裂后的右子节点(树的高度+1)
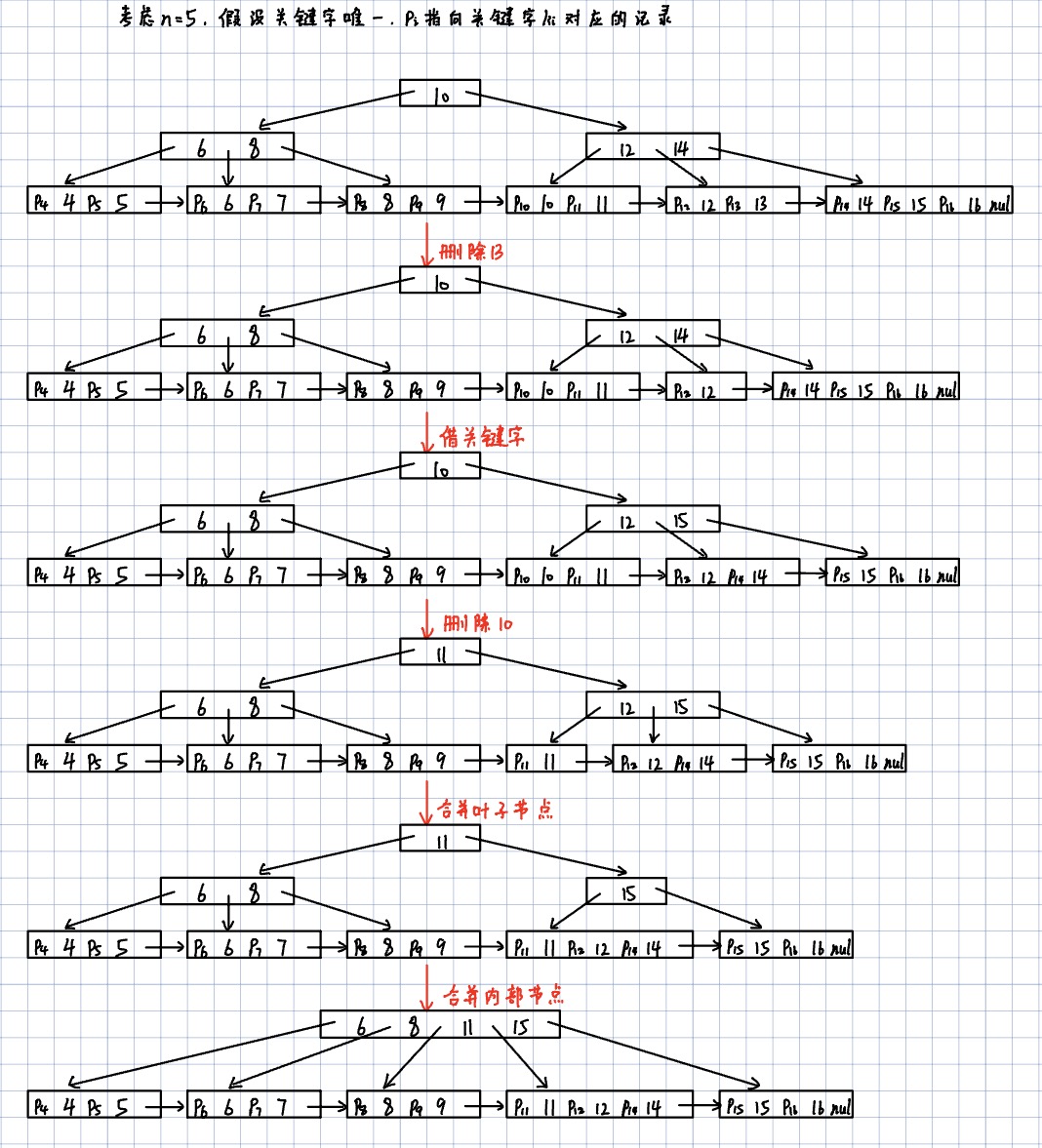
3.5 删除操作
- 寻找目标关键字位置:从根节点出发,根据关键字的顺序递归查找目标关键字所在的叶子节点,如果关键字不存在,删除操作结束,否则进入第2步
- 删除关键字:在目标叶子节点中直接删除该关键字,同时如果该关键字是内部节点的分隔关键字,需要修改分隔关键字为更大的关键字,如果删除后关键字数量大于等于,则删除操作结束,否则进入第3步
- 借关键字:选择左兄弟或右兄弟中关键字数量大于的节点,如果不存在这样的兄弟节点则进入第4步
- 如果是左兄弟节点:借最大关键字,更换父节点中对应关键字为左兄弟节点的次大关键字
- 如果是右兄弟节点:借最小关键字,更换父节点中对应关键字为右兄弟节点的次小关键字
- 合并节点
- 如果有左兄弟节点则合并左兄弟节点,否则合并右兄弟节点
- 如果是叶子结点合并,删除父节点中的对应关键字
- 如果是内部节点合并,将父节点中分隔关键字下移到合并节点中
- 递归处理父节点,直到满足关键字要求或父节点是根节点,进入第5步
- 根节点调整:直接删除空的根节点即可(树的高度-1)
推荐一个可视化B+树的网址:
4. Mysql使用索引
4.1 命令
创建索引
1 | create index 索引名 on 表(属性); |
删除索引
1 | drop index 索引名; |
4.2 存储引擎
| 类型 | InnoDB | MyISAM | MEMORY |
|---|---|---|---|
| 索引类型 | 聚集索引,索引存储数据 | 辅助索引,索引存储指向数据的地址 | 散列索引,数据存储在内存中 |
| 索引结构 | B+树索引 | B+树索引 | 散列索引 |
| 特性 | 支持事务和外键约束 | 适用于以读为主的场景 | 支持极高的查询性能,但不适合范围查询 |
4.3 默认索引
主键索引:添加primary key约束,数据库会自动创建主键索引,是聚集索引
唯一索引:添加unique约束,数据库会自动创唯一索引,是辅助索引