1. 优化定义

优化级别

  • 源代码优化：编写更加高效的代码
  • 中间代码优化：环路不变量提升、全局常量传播
  • 目标代码优化：在具体 CPU/指令集上做与硬件密切相关的调度与分配，比如填充延迟槽、避免流水线冲突

优化类别

  • 局部优化：只在单个基本块内做优化
  • 循环优化：针对环路体处理，基于控制流分析
  • 全局优化：在整个程序范围内的优化，基于数据流分析

2. 通用技术

2.1 删除公共子表达式

如果存在多次计算结果相同的表达式，且第一次计算结果存到了 t，则之后复用 t

1
2
3
4
5
6
x = a*b + c  
y = a*b + d  
简化为
t = a*b
x = t + c
y = t + d

2.2 常量折叠与常量传播

折叠指的是把编译器已经可以计算的算术求值，传播指的是将常量信息沿着数据流往下传播，触发更多折叠

1
2
3
x = 1  + 1		// 折叠：x = 2
y = x + 1   // 传播：y = 3
z = x + y   // 传播：z = 5

2.3 消除死代码

将给变量赋值但之后无引用的指令删除

1
2
3
4
5
6
7
8
9
w = 2
x = 5
y = x      // 赋值，但无引用
z = x + 1
w = w + 1 // w 自己引用自己
x = x + 1
简化为
x = 5
z = x +1

2.4 强度削弱

将成本高的操作换位等价但成本低的操作

1
2
i * 8  转化为 i << 3
i * 10 转化为 (i << 3) + (i << 1)

3. 局部优化

3.1 基本块划分

入口语句

  • 程序的第一个语句
  • 转移目标对应语句
  • 条件跳转后继语句

image-20250622173702190

基本块

  • 入口语句到下一个入口语句到前一条语句
  • 入口语句到转移语句
  • 入口语句到停止语句

image-20250622173721277

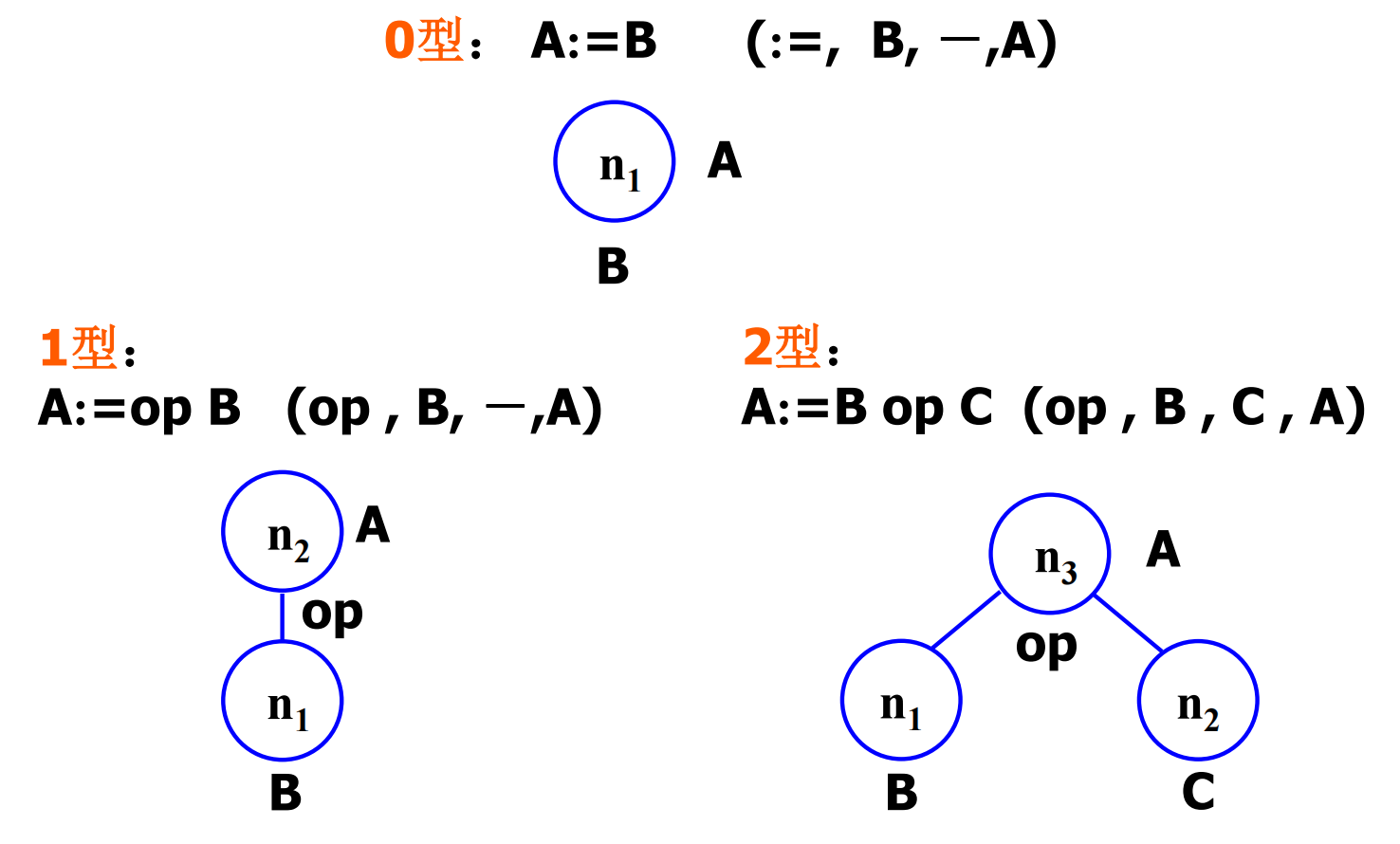
3.2 DAG

构造

  • 内部节点：操作符，代表用该符对其后继结点所代表的值进行运算的结果
  • 叶子结点：操作数，代表变量或常数的值
  • 边：从操作数指向运算节点

image-20250622173830178

构建：按块内指令顺序扫描，对每条 A := B op C

  1. 查找是否已存在代表 B op C 结果的节点，若有就复用
  2. 否则新建叶子节点 B 和 C，新建内部节点 op，op 连接 B 和 C
  3. 按照通用方法对代码进行简化

image-20250622174007273

优化

  1. 若节点的所有叶子都是常量，立即在图上算出结果，替换为常量叶子节点
  2. 识别那些没有任何后续定义或最终写回的节点，直接剪掉

image-20250622174032676

4. 循环优化

4.1 流图

流图

  • 节点：每个基本块
  • 根节点：含第一条语句的节点
  • 边：跳转执行和顺序执行都对应一条边

4.2 代码外提

将循环不变运算提到循环体外

image-20250622174114939

4.3 变换循环控制条件

减少冗余的变量与代码

image-20250622174125650

4.4 确定循环

确定流图中的循环

  1. 计算支配点集：如果从起始点到 n 都必须经过 m，则称 m 支配 n
  2. 计算回边：如果 m 支配 n，但同时又存在一条有向边 n->m，则称 n->m 为回边
  3. 计算循环：如果 n->m 是回边，则所有从 m 出发并到达 n 上的点集构成循环

可归约流图：移除所有回边之后，图是五环的

image-20250622174234520

5. 全局优化

5.1 到达定值数据流分析

到达：变量 A 的定值点 p 到达 q 表示流图存在一条从 p 到 q 的路径，并且路径上不存在 A 的其他定值

数据结构定义

  • B：基本块
  • P[B]：B 的所有前驱基本块
  • S[B]：B 的所有后继基本块
  • IN[B]：到达 B 入口处各个变量的定值点集合
  • OUT[B]：到达 B 出口处各个变量的定值点集合
  • GEN[B]：B 中的定值可以到达 B 出口处的定值点集合
  • KILL[B]：能够到达 B 的入口处，但是在 B 内被重新定值的定值点集合

引用定值链（UD链）：变量的引用来自的定值语句集合

image-20250622174602900

不动点方程

  • IN[B]  =  ⋃b∈P[B]OUT[b]\mathrm{IN}[B]\;=\;\bigcup_{b\in P[B]} \mathrm{OUT}[b]：入口处能看到的定值，就是能到达前驱基本块出口处的定值

  • OUT[B]  =  GEN[B]  ∪  (IN[B]  −  KILL[B])\mathrm{OUT}[B]\;=\;\mathrm{GEN}[B]\;\cup\;\bigl(\mathrm{IN}[B]\;-\;\mathrm{KILL}[B]\bigr)：能到达出口处的定值，就是新生成的定值∪\cup 入口处进来的定值且没有被覆盖的定值

迭代不动点算法

  1. 令 GEN[B] = 内部全部标号
  2. 初始化每个基本块 B，初始化迭代集合为所有按顺序的基本块
    1. IN[B] = ∅
    2. OUT[B] = GEN[B]
    3. KILL[B] = 程序中所有既在基本块 B 定值又在其他基本块定值的标号
  3. 取出迭代集合中按序第一个基本块 B，根据最新的 OUT 情况，先更新 IN[B]，再更新 OUT[B]
  4. 如果确实有更新，则把 S[B] 加入迭代集合
  5. 如果迭代集合为空则停止，否则回到 3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 1. 初始化
for each B:
    IN[B] = ∅
    OUT[B] = GEN[B]

// 2. 迭代求不动点：注意 workset 是集合，不含重复元素
workset = all B in arbitrary order
while workset ≠ ∅:
    // 3. 按顺序拿基本块并弹出
    B = workset.pop()
    
    // 4. 计算 B 新的 IN 和 OUT
    IN_new = ⋃{ OUT[b] | b in P[B] }
    OUT_new = GEN[B] ∪ (IN_new − KILL[B])
    
    // 5. 如果有变化则重新加入
    if IN_new ≠ IN[B] or OUT_new ≠ OUT[B]:
        // 5.1 更新
        IN[B]  = IN_new
        OUT[B] = OUT_new
        
        // 5.2 将所有后继加入
        for each b in S[B]:
            workset.append(b)

image-20250622174519384

5.2 活跃变量数据流分析

活跃：

数据结构

  • Def[B]：在块中对定义了一个新值并且它会屏蔽从入口处传过来的旧活跃值
  • Use[B]：在块中任何定义之前就要用到旧值的变量集合
  • P[B]：B 的直接前驱基本块集合
  • S[B]：B 的直接后继基本块集合
  • LiveIn[B]：到达块入口处活跃的变量集合
  • LiveOut[B]：到达块出口处活跃的变量集合

定值-引用链：变量的定值能过被引用的语句集合

image-20250622175303224

不动点方程

  • LiveOut[B]=⋃s∈S(B)LiveIn[s]\text{LiveOut}[B] = \bigcup_{s \in \mathrm{S}(B)} \text{LiveIn}[s]：如果在后继块入口都活跃的变量，那么在当前块的出口肯定也活跃
  • $ \text{LiveIn}[B] = \text{Use}[B] ;\cup;\bigl(\text{LiveOut}[B];-;\text{Def}[B]\bigr)$：当前块入口活跃的变量，是块内用到的变量∪\cup 原先出口活跃的变量除去被重新定义的变量

迭代不动点算法

  1. 求出每个块的 Def[B] 和 Use[B]
  2. 初始化LiveIn[B]=∅,LiveOut[B]=∅\mathrm{LiveIn}[B] = \varnothing,\quad \mathrm{LiveOut}[B] = \varnothing，初始化迭代集合为所有按顺序的基本块
  3. 按照不动点方程，根据最新的 Livein 情况，先更新 LiveOut[B]，再更新 LiveIn[B]，将有变动的块的前驱块加入迭代集合中
  4. 如果迭代集合为空则停止，否则回到 3

image-20250622175043338